Il Cigno Nero: Volatilità e Rischio di portafoglio

Sintesi

La volatilità è un concetto evanescente e abusato da chi pratica gli investimenti finanziari. Troppo spesso i tecnici di settore usano questo termine senza davvero avere colto il significato, senza conoscerne le origini e neppure le potenzialità o i campi di applicazione. Sono presenti libri di testo e siti internet in cui la volatilità viene trattata con gravi errori concettuali e in termini a volte riduttivi e/o inesatti.

Procediamo quindi a dare una corretta definizione che sia rigorosa sul piano teorico ma soprattutto che sia semplice sul piano intuitivo in modo che possa essere compresa da tutti. Vi saranno rimandi e link per chi volesse approfondire il concetto sul piano matematico-statistico e seguiranno alcune considerazioni personali del sottoscritto Franco Bandelli sui potenziali utilizzi di questo strumento.

Tesi

La Volatilità – misurata dalla formula della Deviazione Standard presa in prestito dalla Statistica  – intesa come rischio di un investimento finanziario è un concetto scorretto e fuorviante.

Non ha alcun senso valutare la volatilità storica di uno strumento finanziario presa singolarmente senza l’ausilio e la analisi contestuale di altri parametri quali ad esempio il rendimento medio conseguito nel lasso di tempo oggetto di studio e altre metriche quali lo Sharpe Ratio, il Max Drawdown, pena il rischio di giungere a conclusioni totalmente errate.

Approfondimento

È noto che la finanza, intesa come disciplina che mira ad impiegare il denaro effettuando investimenti finalizzati a conseguire un profitto, poggia le sue basi teoriche su discipline apparentemente assai diverse fra loro, la psicologia e la statistica, solo per citarne alcune.

Affrontiamo ora il tema in oggetto: la negazione della Volatilità storica – come valore preso a sé stante – quale misura del rischio di un investimento.

Definiamo innanzitutto il concetto di volatilità nell’ambito degli investimenti finanziari come la variazione o la oscillazione che un titolo o altro strumento finanziario può subire sia in senso positivo che negativo in un arco definito di tempo intorno ad un valor medio. Forti oscillazioni di un titolo, secondo la dottrina finanziaria universalmente e attualmente riconosciuta, sono quindi associate ad alta volatilità, quindi ad un alto rischio.

Precisiamo che esistono due tipi di volatilità: la volatilità storica oggetto di questo articolo e la volatilità implicita che sarà trattata in separata sede.

Nota Bene: chi sin da bambino ha fatto a pugni con la matematica o con la statistica, salti la parte sottostante scritta in corsivo – anche se presentata in modo assai semplice – e prosegua oltre, sebbene personalmente ritengo sia importante leggerla ai fini della comprensione dei concetti successivi.

La volatilità può e deve essere misurata per effettuare ragionamenti sulle strategie da impostare per effettuare gli investimenti. Sulle modalità di misurazione ci viene in soccorso la Statistica che tramite formule matematiche ci permette di quantificarla – ad esempio – tramite la formula della Deviazione Standard.

In statistica la Deviazione Standard (dagli amici chiamata Sigma e dai matematici Scarto Quadratico Medio) è un indice statistico di dispersione che misura – in una serie di valori casuali cioè aventi una distribuzione normale – la dispersione di ogni valore rispetto alla media (Mi) dei valori stessi.

Rimandiamo i lettori amanti della statistica e delle formule matematiche al seguente link per approfondimenti sulla curva gaussiana e distribuzione normale. https://it.wikipedia.org/wiki/Distribuzione_normale

A livello concettuale concentriamoci invece sulla figura sottostante che rappresenta una serie di valori distribuiti in modo casuale. Si noti che la linea blu definisce la media dei valori mentre le righe parallele rosse soprastanti e sottostanti la linea blu delimitano l’area nella quale cadono i valori posizionati alla distanza di UNA deviazione standard dalla media.

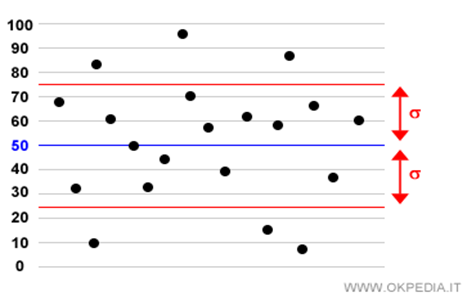
E’ possibile rappresentare graficamente la formula statistica della Deviazione Standard – che misura la Volatilità – tramite la figura sottostante della campana gaussiana sulla base di una serie di valori distribuiti in modo normale:

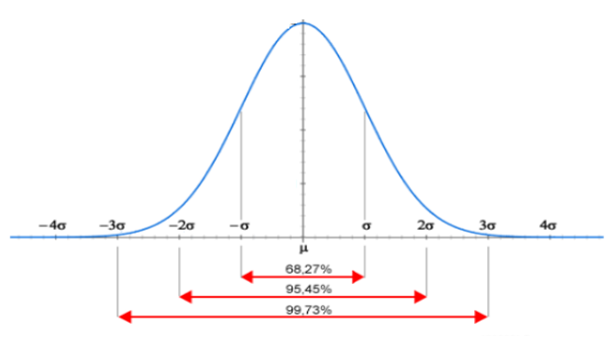
L’analisi del grafico mostra che la maggior parte dei valori (precisamente il 68,27%) di una serie numerica distribuita in modo normale, ad esempio quelli disegnati nella figura precedente, cade all’interno della campana gaussiana, sia nella parte destra che sinistra, nella area compresa tra la media (Mi) e UNA deviazione Standard (Sigma). Vi sono valori invece che si discostano molto di più dalla media, ad esempio quei valori compresi tra -2 e -1 e +1 e+2 Deviazioni Standard ma sono molto meno frequenti e posizionati in una area più piccola della campana. Possiamo leggere il grafico verificando anche che i valori più lontani dalla linea perpendicolare rappresentante la media (Mi) dei valori delle letture di una serie numerica hanno una maggiore dispersione e sono più rari. O alternativamente che il 95,45% dei valori di una serie cadono dentro l’area compresa tra la media MI e -2 e + 2 deviazioni standard Sigma.

Da notare anche che una curva gaussiana avente una campana stretta indica che la dispersione dei valori è molto concentrata vicino alla media, ciò significa che avremo un valore di Deviazione Standard (o Volatilità) basso. Da ciò ne segue che una gaussiana bassa e larga indica che i valori di una serie numerica sono dispersi molto lontano dalla media ed avremo valori numeri della Deviazione Standard (Volatilità se parliamo di investimenti finanziari) molto elevati. La altezza della campana dipende dalla frequenza con cui i valori oggetto di studio si presentano. Una campana molto alta e larga è indice di una frequente e ampia dispersione dei valori intorno al valor medio.

Dopo questi brevi cenni di Statistica, per la gioia dei lettori senza mostrare alcun calcolo matematico o formula matematica a supporto di quanto esposto, torniamo alla Statistica applicata alla Finanza. L’industria del risparmio gestito ha da sempre cercato di quantificare il rischio di un investimento tramite valori numerici e l’utilizzo della Deviazione Standard (che da questo istante sarà definita come Volatilità) ha effettivamente un senso.

La base del ragionamento sta nel fatto che le oscillazioni di uno strumento finanziario, ad esempio i valori di chiusura di borsa, posso essere intesi come una serie di valori aventi una distribuzione normale o casuale e quindi sottostanti alle leggi della Statistica sopra esposte. In effetti l’evidenza empirica suggerisce che per la maggior parte del tempo le quotazioni di un titolo si muovono senza una direzione apparente oscillando più o meno ampiamente e casualmente intorno ad un valor medio.

Se seguiamo questa linea di pensiero stiamo implicitamente sposando la Teoria del Random Walk dei mercati, altrimenti conosciuta dome “Camminata dell’Ubriaco” e stiamo accettando come provata la Teoria della Efficienza dei Mercati  secondo la quale i mercati sono efficienti e i prezzi di un titolo riflettono tutte le informazioni sul mercato e che queste siano disponibili per chiunque.

Personalmente – pur rispettando l’impianto teorico di queste teorie economiche – rinnego la validità di questi approcci al mercato. Il fatto di NON accettare questi postulati – l’efficienza dei mercati e la casualità delle oscillazioni – porta inevitabilmente a negare che la Volatilità sia una valida misurazione del rischio di un investimento se considerata come unico parametro di valutazione.

Focalizziamo ora l’attenzione su due possibilità diverse.

1 – Caso: Mercato volatile con rendimenti costantemente negativi o positivi

Supponiamo di avere due potenziali investimenti, uno dei quali presenta dei rendimenti compresi tra -5% e + 30% ed un altro che offre rendimenti compresi tra -30% e +5%. È agevole intuire che la volatilità è identica anche se il primo di essi è palesemente meno rischioso. Senza scomodare la calcolatrice si intuisce immediatamente che nel primo esempio le oscillazioni si concentrano intorno ad una media di valori tendenzialmente positivi mentre nel secondo caso i rendimenti sono posizionati sulla parte negativa dei rendimenti.

La figura sottostante ci aiuta a capire meglio quanto appena riportato.

Si noti che tra le 4 gaussiane disegnate, quella in verde spostata a sinistra rappresenta bene il concetto. Siamo in presenza di una Volatilità positiva (lo sarà sempre in quanto la formula matematica della Deviazione Standard eleva i valori al quadrato e per questa ragione la testa della campana è posizionata sempre sopra i valori di zero) ma i valori dei rendimenti sono assiepati intorno a un valor medio negativo. Certamente questo non è un buon investimento !

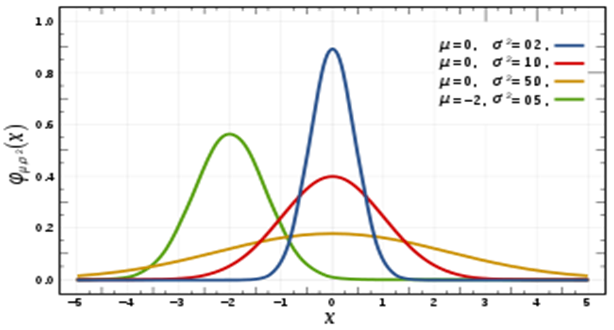
Sapendo che nel caso descritto la volatilità dei due investimenti è identica, come usciamo dal tunnel in cui siamo finiti? A parità di volatilità, quale investimento dovremmo preferire? Dobbiamo per forza fare appello ad almeno un altro parametro quale, ad esempio, il rendimento medio. A parità di Deviazione Standard sarà ovviamente preferibile l’investimento con rendimento maggiore, da ciò segue anche che nella valutazione di due investimenti, a parità di rendimenti è preferibile quello avente una volatilità minore (non fosse altro perché aiuta i deboli di cuore nel sopportare meglio le eventuali ampie oscillazioni).

 Il vero rischio degli investimenti non può essere valutato ed evidenziato – come spesso accade – solamente da una volatilità con alti valori (nelle figure gaussiane è rappresentata da una campana molto larga) ma dalla frequenza dagli scostamenti in negativo rispetto alla media.  Sono proprio questi scostamenti che si traducono poi in perdite effettive.

Da quanto esposto possiamo prendere atto che possono esistere investimenti molto volatili ma poco rischiosi ed investimenti poco volatili ma rischiosi e non solo, come spesso ed erroneamente si crede, rendimenti molto volatili e molto rischiosi.

La figura sottostante mostra, ad esempio, un grafico in rosso relativo ad un investimento molto volatile e poco rischioso rispetto al grafico in colore blu relativo a un investimento poco volatile ma meno redditizio.

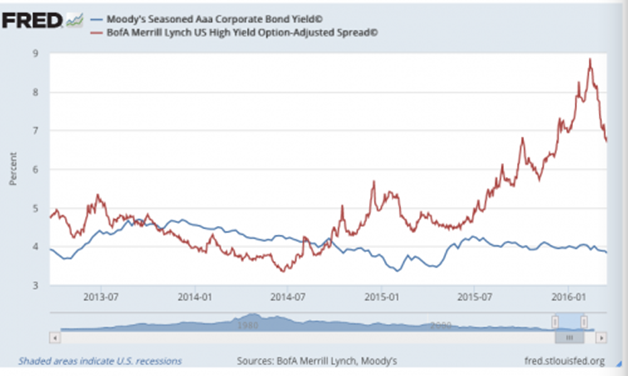
2 – Caso: Volatilità alta o bassa con mercato direzionale

Questo esempio, dalla cui analisi dei dati si evidenzia una sequenza di valori tipica di un trend al rialzo, presenta una diversa ma possibile realtà.

Per semplicità, supponiamo di avere dei prezzi mensili di chiusura di un titolo da $ 1 a $ 10. Ad esempio, il mese uno è $ 1, il mese due è $ 2 e così via sino al decimo mese. Dopo aver applicato le formule e effettuato gli opportuni calcoli, risulta che il valor medio è 5,5 e il risultato della Deviazione Standard è 2,87. Secondo le figure e la teoria precedentemente esposta se i prezzi di chiusura fossero distribuiti in modo casuale – e in questo caso non lo sono – il 68% dei valori sarebbe compreso in UNA deviazione standard (cioè 2.87) e il 95% in DUE deviazioni standard (2×2.87).

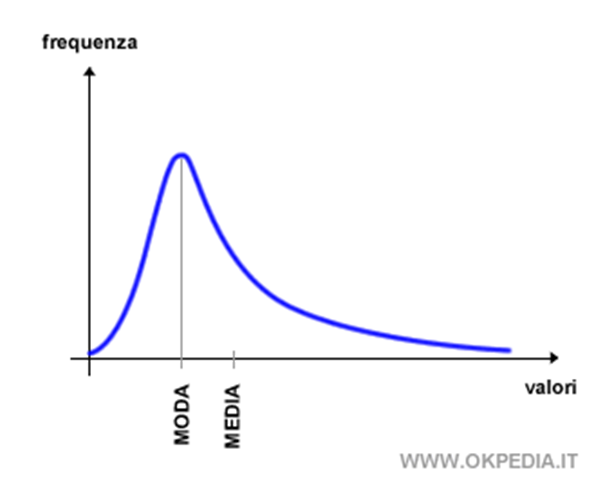
È facile intuire che in questo caso, i valori da $1 a $10 non vengono distribuiti in modo normale su una curva a campana; infatti, c’è un significativo orientamento al rialzo., quindi tutti i valori non rientrano nelle deviazioni standard ipotizzate dalla statistica. Un grafico disegnato sulla base di questi valori mostrerebbe una asimmetria e un ispessimento della coda nella parte destra della campana con una maggiore area nella parte sinistra rispetto al medio, come da figura sottostante.

CONCLUSIONI

La analisi dei rendimenti passati di un titolo o altro strumento finanziario ha spesso una distribuzione NON NORMALE, pertanto, accade che la distribuzione dei valori (ad esempio i rendimenti di un portafoglio in finanza) non sia casuale.

Nel caso ciò accadesse – e le motivazioni potrebbero essere le più disparate – significa che la forma della curva Gaussiana non è a campana come la statistica ci insegna e quindi ne consegue che:

– non è sempre vero che il 68% o il 95% dei rendimenti passati è compreso rispettivamente in UNA o DUE Deviazioni Standard (vedi ad esempio i valori di un trend al rialzo o ribasso).

– non è sempre vero, che ad alti valori di volatilità corrispondano alti rischi (vedi ad esempio rendimenti medi molto contenuti ma ampie oscillazioni intorno al valor medio).

Inoltre, vale appena la pena di sottolineare che la volatilità storica è FUNZIONE delle dispersioni intorno al valor medio. Cosa significa? Significa che il valore della volatilità, espresso dalla Deviazione Standard, è dinamico, non è mai identico a sé stesso e varia al trascorrere del tempo a seconda della ampiezza delle oscillazioni delle quotazioni avvenute in passato e di quelle che seguiranno in futuro.

Quanto detto spiega bene la presenza in finanza del tanto temuto Black Swan (o Cigno Nero per noi italiani). Sino al 1697, data in cui abbiamo appreso la presenza, si credeva che i cigni neri NON esistessero oppure fossero frequenti quanto le mosche bianche.

Fino a quando in Australia si è scoperto un lago popolato da cigni neri.

In finanza il Black Swan fa riferimento ad un evento assolutamente improbabile o imprevedibile sulla base delle conoscenze o dei dati storici sino a quel momento in possesso.

Se volessimo rappresentare il concetto su una curva gaussiana a campana stiamo parlando di eventi neppure compresi fra le 3 Deviazioni Standard (99.73% dei casi), valore rarissimo e molto vicino alla impossibilità.

L’evidenza ci insegna che nell’ambito degli investimenti finanziari i cigni neri esistono e palesano la loro cupa presenza in modo molto più tragico e frequente di quanto non si pensi, la realtà infatti sa essere di solito ben più drammatica di quanto la statistica e il calcolo delle probabilità possano ipotizzare perché queste discipline raccontano una verità passata sulla base dei dati storici e non possono contemplare eventi non ancora accaduti.

I libri di storia sono pieni di Cigni Neri che svolazzano come passerotti nei cieli della Economia.

CONSIDERAZIONI PERSONALI

La volatilità storica è un utile parametro per effettuare valutazioni su serie storiche di dati, ma non ha affatto alcuna capacità predittiva sugli eventi futuri.

Per facilitare il lettore, si immagini di guidare una vettura in autostrada e guardare dallo specchietto retrovisore i movimenti delle automobili retrostanti e ci accorgiamo che dietro di noi vi è traffico e una lunga colonna di automobili che ci segue. La volatilità ha questa funzione nella analisi degli andamenti finanziari. Analizzare il passato senza avere la certezza che questo si ripresenti nell’immediato futuro e piuttosto cercare di analizzare le probabilità – più o meno alte – che quanto già accaduto possa accadere di nuovo soprattutto nel brevissimo periodo. Tornando all’esempio della vettura in autostrada, se lo specchietto retrovisore mostra che vi è traffico dietro di noi, probabilmente vi sarà traffico anche di fronte a noi e quindi vedremo una lunga coda di vetture ma ciò non è affatto certo, soprattutto se siamo noi stessi il tappo che crea l’ingorgo.

Fuor di metafora, se consideriamo un investimento con un rendimento annuale medio del 7% e una volatilità del 3% (valore notoriamente basso in ambito di investimenti finanziari) e volessimo utilizzare la volatilità storica in funzione predittiva, in base alla rappresentazione di una curva gaussiana i valori di chiusura del giorno successivo saranno compresi al 68% di probabilità (cioè UNA deviazione standard) in una oscillazione tra -3% e +3% rispetto al valor medio calcolato.

Quanto detto sarà probabilmente vero grazie alla analisi dei valori storici ma ciò non toglie che un evento infausto, ad esempio un attentato terroristico avvenuto a borse chiuse, non possa far crollare le quotazioni del 12% all’apertura del giorno successivo. Ciò accade molto più spesso di quanto non si creda.

Vogliamo menzionare qualche evento?

• Nell’ottobre 1987 l’indice S&p500 perse il 23% nel giorno ricordato tristemente come Black Monday.
• Durante la crisi economica e finanziaria degli anni 2007-2008 gli indici dio borsa avevano oscillazioni giornaliere anche del 20% !!
• Nel Giugno 2016, in occasione della Brexit dopo l’esito non previsto del referendum, il cross sterlina/euro scese di ben 25 Deviazioni Standard !
• Nel marzo 2020 l’indice italiano Ftsemib40 scese del 40% in poche settimane.

La lista degli eventi infausti è lunga ma ovviamente è ben chiaro che la realtà si è presa molte volte gioco della statistica, delle teorie sulla probabilità e di tutti gli indici che misuravano la volatilità.

APPROCCIO METODOLOGICO

Chiarito che conoscere solamente la volatilità storica di uno strumento finanziario non aiuta a valutare correttamente il rischio, proponiamo un semplice ma non esaustivo approccio metodologico:

1 – Nel caso che il nostro promotore finanziario o la nostra banca ci proponga un investimento, sappiano i lettori che solitamente vengono messi in luce i rendimenti positivi passati avendo cura di minimizzare i rischi assunti per ottenerli. Perfino Lorenzo dei Medici – pur non capendo nulla di investimenti finanziari – nella Canzona di Bacco del 1490 suggeriva prudenza, scriveva infatti: “Chi vuol esser lieto, sia: di doman non c’è certezza”

2 – In merito alla proposta di investimento, è importante conoscere i valori espressi in percentuale sia della volatilità storica che del rendimento annuale conseguito. A parità di rendimento preferire quello con volatilità minore o in alternativa a parità di volatilità focalizzarsi su quello con rendimento maggiore. Ad esempio: se due fondi di investimento rendono su base annua il 5% ma il primo ha volatilità 3% e il secondo ha volatilità 4%, preferire il primo. Inoltre, preferire sempre investimenti che abbiano un rendimento % maggiore della volatilità % rispetto al contrario.

3 – E’ fondamentale conoscere il Max Drawdown degli ultimi 10 anni, se possibile. In sostanza bisogna valutare se i crolli avvenuti nel passato sono compatibili col nostro profilo di rischio e se sono accettabili dai nostri nervi. In caso di crollo dei mercati non tutti sono disposti a vedere perdere un 30% in pochi giorni pur sapendo che in passato l’investimento avrebbe poi recuperato quanto perso in precedenza.

4 – Nella valutazione dell’investimento è importante conoscere il valore del Underwater Time. Significa sapere dopo quanto tempo l’investimento in fase di crollo ha recuperato tutte le perdite. E’ ovvio che avere 90 anni e investire in fondi di investimento che in passato hanno recuperato le perdite dopo 15 anni non frega nulla a nessuno !!

5 – Chiedere al Promotore Finanziario di conoscere il V.A.R.  dell’investimento, acronimo di Value At Risk. In sostanza si vuol sapere quale sarebbe la perdita massima potenziale, misurata in termini di probabilità e definito un determinato arco temporale, che l’investimento subirebbe in caso di eventi infausti. Ad esempio: se il Var 95 ad un giorno è di 1.000 Euro significa sapere che in un giorno il nostro portafoglio potrebbe perdere non più di 1.000 Euro con una probabilità non superiore al 95%. Ciò può anche significare che nel rimanente 5% di probabilità non contemplate dal Var può accadere di tutto, anche che appaia il temuto Cigno Nero.

6 – Chiedere al Promotore Finanziario di conoscere l’indice di Sharpe e preferire investimenti con valori maggiori di 1. Lo Sharpe Ratio mette in relazione il rendimento di un investimento con la volatilità per averlo conseguito considerando anche il valore di un investimento privo di rischio (quale ad esempio un Bot a tre mesi). In sostanza l’indice segnala quanto rendimento percentuale offre un investimento per ogni unità di rischio espressa dalla volatilità. Semplifichiamo di molto con un esempio: se due fondi rendono rispettivamente il 10% con volatilità al 8% e il 7% con volatilità al 5% e consideriamo nullo il rendimento di un investimento privo di rischio (a causa della attuale politica ultra-espansiva delle Banche Centrali cha hanno abbattuto i tassi di interesse) la valutazione dei due fondi si riduce al semplice confronto dei seguenti rapporti 10%/8% = 1,25 e 7%/5% = 1,4. Significa che è preferibile il secondo investimento con Sharpe Ratio maggiore anche se rende il 7%, in quanto meno rischioso del primo avente il 10% di rendimento.

7 – Non dimentichiamo mai che ogni investimento deve essere valutato con attenzione, con prudenza e con metriche e indici differenti. I risultati devono essere in ogni caso contestualizzati e mai presi come verità assoluta.

E ricordiamoci sempre che il Cigno Nero è costantemente in agguato!